递推关系

递推关系模型[需补充]

从兔子数列到牛数列

汉诺塔

满足特定条件的01串（如，不包括连续两个0的01串）

（卡塔兰数的一种情形）n个数相乘的顺序总数

递推算法[需补充]

讲座问题

动态规划

线性递推

齐次

所谓线性齐次常系数递推关系（linear homogeneous recurrence relations with constant coefficients），指的是形如$a_n = c_1 a_{n-1} + c_2 a_{n-2} + … c_k a_{n-k}$的递推关系。

提到“线性齐次常系数递推关系”我们就会提特征方程与特征根，它们是用以解递推式的利器。

特征根是个非常有效但也让人摸不着头脑的东西。它本身有何意义？下面笔者粗浅地谈谈自己对其的认识。

二阶递推式[需完善]

如果递推式形如$a_n = Aa_{n-1} + Ba_{n-2}$，$a_n$该如何解呢？我们考虑能否用特殊的$a_n$凑出答案，比如，$a_n = x^n$，这样？把它代入原递推式，我们得到一个二次方程$x^2 - Ax - B = 0$，如果它有不同的解$x_1, x_2$，诶，好，$a_n = x_1^n$或者$a_n = x_2^n$看上去都可以。

但是啊，$a_n = Aa_{n-1} + Ba_{n-2}$是由$a_1, a_2$完全确定的。如果$a_1 \not = x_1$，那不就出问题了吗？其实，前面说$a_n = x_1^n$“可以”，那么$a_n = Cx_1^n + Dx_2^n$也是“可以”的。这样便能够通过给定的$a_1, a_2$解一解C、D，$a_n$的通解也就出来了。

因为$x^2 - Ax - B = 0$和$a_n$有着密切的联系，我们称前者为“特征方程”。

以上是特征方程有两个相异根的情形，如果相同则如何呢？不一定存在$C$使得$a_1 = Cx_1$且$a_2 = Cx_1^2$啊！在这个条件下，我们令$a_n = Cx_1^n + Dnx_1^n$。可以证明，这样的$a_n$满足条件//为什么想到要这样做？

n阶递推式

与上面类似的，我们能想到无重根的n阶递推式的通解形如$a_n = \sum\limits_{i = 1}^k \alpha_i r_i^n$，其中$r_i$为特征方程的解。

至于有重根的n阶递推式，它则形如$a_n = \sum\limits_{i = 1}^k(\sum\limits_{j = 0}^{m_i} \alpha_{(i, j)} n^j r_i^n)$，其中$r_i$为特征方程的解，$m_i$为重数。

证明呢？不管了(¬､¬)

有重根的n阶递推式

非齐次[需完善]

所谓线性非齐次常系数递推关系（linear nonhomogeneous recurrence relations with constant coefficients），指的是形如$a_n = c_1 a_{n-1} + c_2 a_{n-2} + … c_k a_{n-k} + F(n)$的递推关系。

思路

找特解，而后化归到齐次。（这些方程都这种套路，得归纳一下）

特解怎么找呢？比如$a_n = 3a_{n-1} + 2n$，我们可以从结构上猜出$a_n = Cn$。而对于$a_n = 5a_{n-1} - 6a_{n-2} + 7^n$，我们也可以猜一个$a_n = C \cdot 7^n$。但是如果是$a_n = 5a_{n-1} - 6a_{n-2} + 3^n$，$a_n = C \cdot 3^n$就不管用了，要$a_n = C \cdot n^2 \cdot 3^n$才行（为什么又是这个形式？我不知道）。

一般的，有下面的定理。

定理

若$a_n = c_1 a_{n-1} + c_2 a_{n-2} + … c_k a_{n-k} + F(n)$，$F(n)$形如$(b_t n^t + b_{t-1} n^{t-1} + … + b_1 n + b_0) s^n$，其中b、s均为常数。递推关系的特征方程$x^n - c_1 x^{n-1} - c_2 x^{n-2} - … c_k x^{n-k} = 0$的解中s的重数为m，则特解的形式形如$a_n = n^m (p_t n^t + p_{t-1} n^{t-1} + … + p_1 n + p_0) s^n$。

我不会，就不证了例子：$a_n = 6a_{n-1} - 9a_{n-2} + F(n)$，当$F(n)$分别取$F(n) = 3^n, F(n) = n 3^n, F(n) = n^2 2^n, F(n) = (n^2 + 1) 3^n$，求$a_n$的通解。

应用：如求$a_n = \sum n^k$。

分治算法

研究分治算法时，一个值得关注的对象是时间复杂度。下面举几个大家耳熟能详的例子。

例子：矩阵乘法、二进制乘法（汇编乘法？）、二分查找、归并排序

上面的例子看似相似，但其算法复杂度可以很不一样！最后的公式会依据递推关系中的常数专门进行分类讨论，而且结论虽然能推，但是并不好记。//如何认识这一结论？

关于复杂度的推导，我们可以先简化问题，因为只要得到$f(n) = O(g(n))$就好了，可以对n进行“适当”的放大。这里，我们考虑$n = b^k$。

f(n)的复杂度估计[需完善]

定理1

对于形如$f(n) = af(n/b) + c$的递推式，有

………………..$a = 1 \Rightarrow f(n) = O(log n)$

………………..$a > 1 \Rightarrow f(n) = O(n^{log_b a})$

………………..$a < 1 \Rightarrow f(n) = O(1)$

第一项很好理解，第二项是怎么得到的呢？其实直接得到的是$f(n) = O(a^k)$，而通过换底公式能得到$a^k = n^{log_b a}$，因为我们喜欢把n放到真数的位置。下面也是要用到这个转换的。

定理2

对于形如$f(n) = af(n/b) + cn^d$的递推式，有

………………..$a = b^d \Rightarrow f(n) = O(n^d log n)$

………………..$a < b^d \Rightarrow f(n) = O(n^d)$

………………..$a > b^d \Rightarrow f(n) = O(n^{log_b a})$

典例：最近点对问题[需完善]

计算几何的一个毒瘤经典例题，初看非常的抽象，下面我试着以直观的方式说明一下如何用分治法解决这个问题。

首先分治呢，要先“分”，而后“治”。“分”的话二分比较常见，但二分要在有序集里才好进行。考虑以x坐标对这些点进行排序，然后取中间的点作为分界就好了。

下面的思路有些跳跃，我们从最后的算法出发来反推，这样可能更容易理解些。

分治法大框架的伪代码如下，一些细节先不必理解：

1
2
3
4
5
6
7
8
9
10
double closest(Point p[], int low, int high)
{
    if(high - low == 1 or 2)...
    int mid = (low + high) / 2;
    double d1 = closest(p, low, mid);
    double d2 = closest(p, mid + 1, high);
    double d = min(d1, d2);
    d = merge(...);
    return d;
}

上面框架的细节主要是这个：d = min(d1, d2)。为什么要先算d呢？

这实质上是用于提高效率的。你想，“分”做好了，就是左右两边的最近点对距离都已经分别算出来了，“治”要怎么做呢？枚举左边的点和右边的点的距离么？这样还是$O(n^2)$，算法的复杂度还是没有降低呀！于是我们得限制枚举的点的数量。聪明的Preparata和Shamos发现，如果先算出d1、d2和d，那么用要枚举点的话，只要在下图中两条红线间的区域间（x坐标距mid为d的区域内）枚举即可。

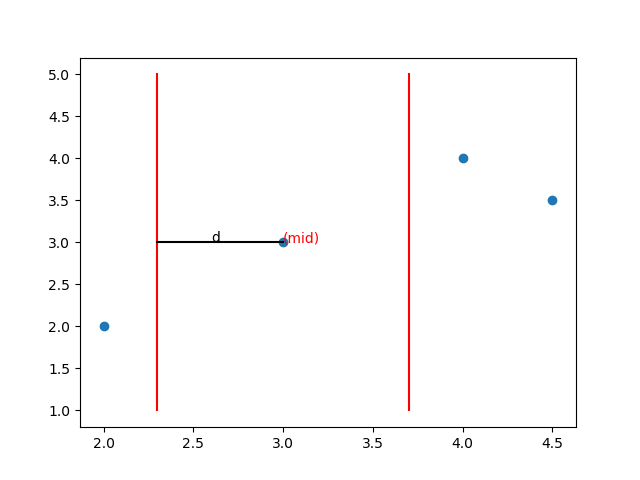
就是说，这里用到了剪枝：把一些分居左右而距离必定超过d的点对剪掉。这个剪枝还是比较宽的，但它容易想到呀，如果要更深入地剪就要深入探究点的结构了，太复杂啦！我们不考虑。

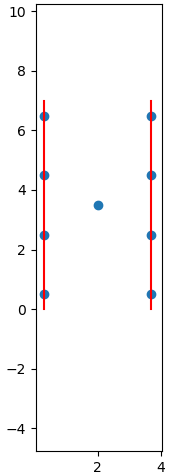
可是，看这张图，即便上面有剪枝，枚举量还是太大了呀，如何缩减呢？我们遇到的问题是这些剩下的点还是无序的，只得暴力枚举，而没有有效的降低枚举量的技巧。于是，聪明的Preparata和Shamos又把剩下的点有序化了，并利用“两点间距离不能大于d”继续剪枝。请看伪代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
double merge(Point p[], int low, int mid, int high, double d)
{
    int len = 0;// the size of the array "temp"
    Point temp[];// the points between the red lines
    
    //branch-cutting 1
    for(int i = low;i <= high;i++)
        if(p[i].x >= p[mid].x - d)
        if(p[i].x <= p[mid].x + d)
        	temp[len++] = p[i];
    
    // the merge part
    sort(temp, temp + len, cmp_y);
    for(int i = 0;i < len;i++)
    {
        for(int j = 1;i + j < len;j++)
        {
            if(temp[i+j].y - temp[i].y > d) break;// branch-cutting 2
            d = min(d, dist(temp[i], temp[i+j]));
        }
    }
}

注意上面“branch-cutting 2”这一行，它很容易理解，但是否足够有效呢？是否存在某组数据使得“the merge part”的运算量退化到$n^2$呢？幸运的是，它足够有效！而且运算量至多是7n！请看下面的图示。

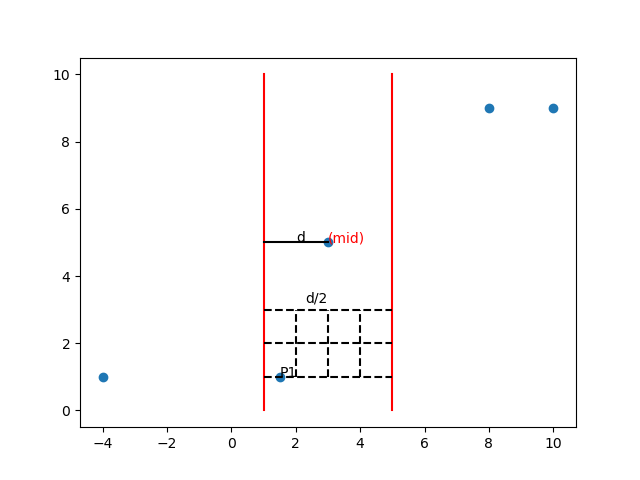
假设我们正枚举到$P1$。Preparata和Shamos证明了，至多有7个$P2$满足$P2.y - P1.y \leq d$。因为前面在左右两边已经”分“过了，故有closest(left), closest(right) >= d，即在“一边”的点两两距离大于d。这个结论非常有用！因为前面已经构造出了以2d为边长的长方形作为我们选点的区域，我们再在这个长方形里画小的正方形，再把P1放进去。能够发现，在图中所示的八个虚线区域中，每个区域至多一个点（否则矛盾）。故而“branch-cutting 2”在至多7步后就会退出，这个剪枝足够有效！

上面的分析还是比较粗略的，因为实际运算时似乎用不着7步，我们能否证明对每个点至多只要4次或5次比较呢？不论如何，总之都是较小的常数就是了。

接着来分析一下算法复杂度吧。开始的按x排序：O(nlogn)，之后的递推：f(n) = 2f(n/2) + nlogn + 7n（nlogn是按y排序）。解上面的递推式，得f(n) = O(nlogn)//为何网上有说法是nloglogn？

以反推的方式理解了一下这个算法，我们再来正面地总结一下我们的步骤：

①准备，按x排序原数组，使之有序；

②“分”，以中点为界，得到两子域中的最短点距；

③“治”，依据②中的最短点距d找出需要枚举的点，这里进行了第一次剪枝；

④“治”，将③中得到的点按y排序，顺序枚举，并通过y的距离进行第二次剪枝；

以上。

总而言之，这个算法的步骤还是容易实现的，难的是深入地理解它。这里两个剪枝分开来看都可能是效率不高的，但合在一起就产生了奇妙的相互作用，保证了总体剪枝的有效性。这十分精妙，但也很难想到，而且不好推广。

另外书上的算法是设了两个数组，分别对x排序与对y排序，之后在后者这一数组中检索，但这样细节是如何处理的呢？我还不知道。

算法的完整代码见下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
struct Point{double x, y;}Points[maxn], temp[maxn];
bool cmp_x(Point &lhs, Point &rhs){return lhs.x < rhs.x;}
bool cmp_y(Point &lhs, Point &rhs){return lhs.y < rhs.y;}
double dist(Point &lhs, Point &rhs)
{
	return sqrt((lhs.x - rhs.x)*(lhs.x - rhs.x) + (lhs.y - rhs.y)*(lhs.y - rhs.y));
}
double merge(int low, int mid, int high, double d)
{
	int len = 0;
	double mid_x = Points[mid].x;

	for(int i = low;i <= high;i++)
		if(Points[i].x >= mid_x - d)
		if(Points[i].x <= mid_x + d)
			temp[len++] = Points[i];
	sort(temp, temp + len, cmp_y);//in the book, it's not necessary to sort. Why?

	for(int i = 0;i < len;i++)
		for(int j = 1;i + j < len && (temp[i+j].y - temp[i].y <= d);j++)
			d = min(d, dist(temp[i], temp[i+j]));
	return d;
}
double closest(int low, int high)
{
	if(high == low) return INF;
	if(high - low == 1) return dist(Points[low], Points[low+1]);
	int mid = (low + high) / 2;
	double d1 = closest(low, mid);
	double d2 = closest(mid + 1, high);
	double d = min(d1, d2);
	return merge(low, mid, high, d);
}
int main()
{
	...//scanf
	sort(Points, Points + n, cmp_x);
	...//printf
}

小结

①分治算法在不同递推式下算法复杂度可能不同，需特殊情况特殊分析。

②分治算法的精髓在于“分而后治”，“分”是“治”的基础，通过“分”得到的有效信息能够帮助我们降低“治”部分的复杂度。在归并排序中，“分”得到的有效信息是子序列的有序性；在最近点对问题中，“分”得到的有效信息是子区域的最近点对距离。

③分治算法本身不难理解，但比较难想到，也比较灵活。分析分治算法时“为何这种问题可以用分治处理”。

生成函数

何谓生成函数？这是个比较玄妙的问题，它的定义很简单，但为何要这样定义，及它为何能用来解决组合问题，则常常会给人带来迷惑，下面笔者以个人的理解粗略地讲讲生成函数。

生成函数的概念

先来看这样一个例子：$x_1 + x_2 + x_3 = 7$，其中$0 \leq x_1 \leq 2, 2 \leq x_2 \leq 3, 3 \leq x_4 \leq 4$，$x_1, x_2, x_3$为整数。求$(x_1, x_2, x_3)$有多少种可能。

我们固然可以通过解答树得到答案，但是否有其他更“代数”的做法呢？考虑这个式子：$(1 + x + x^2) \cdot (x^2 + x^3) \cdot (x^3 + x^4)$。它意味着什么？我们把第一个括号中x的指数看作$x_1$的取值，第二三个括号同理。从一二三个括号中各选一项乘起来，恰好对应$x_1 + x_2 + x_3 = k$的一种方法。故$(1 + x + x^2) \cdot (x^2 + x^3) \cdot (x^3 + x^4)$展开式中$x^k$的系数，即$x_1 + x_2 + x_3 = k$的方法数（而指数所对应的便是$x_1 + x_2 + x_3$的取值）。特别的，取k = 7，就得到了上面问题的答案。

这个方法看上去和暴力枚举并无二致，但事实并非如此。首先，生成函数将组合问题与代数问题连接起来，从而使得组和问题更易表示，而能为计算机所处理（多项式乘法）。其次，这样的算法在运算时更为容易，因为我们更熟练于多项式的乘法而不是列出解答树。

为何上述做法能建立从组和到代数的一一映射呢？原因在于乘法法则与加法法则——$ax^c + bx^c = (a+b)x^c$，这对应于加法法则；$ax^c \cdot bx^d = ab x^{c+d}$，这对应于乘法法则。如果认为这有些抽象，不妨在上面的例子中找找哪里用到了这两个法则。生成函数之所以能够解决组合问题，原因就在于多项式的运算能有这样和组和相关的性质。

上面的生成函数$G(x) = (1 + x + x^2) \cdot (x^2 + x^3) \cdot (x^3 + x^4)$是有限项的，容易理解。但是实际运用中我们一般会考虑无穷项的情况，即将$G(x)$写作无穷级数的形式。然后玄学东西又来了：比如$G(x) = \sum\limits_{i = 0}^{\infty} x^i = \dfrac{1}{1-x}$。为什么可以这样做？这样做有什么好处？这些我们将在下文中，结合具体的案例进行探讨，此时先不要被它迷糊了头脑。

用生成函数证明组和恒等式[需完善]

使用生成函数时，我们需要考虑“意义”。这不是指x的意义——x毫无意义，我们引入x只是要利用多项式的运算，因为它是好的。此处的意义指的是我们运算式子中的意义。拿上面的例子来说，$((1 + x + x^2)), (x^2 + x^3)$分别都有意义，它们相乘也是有意义的。谈到”意义“，你可能想到了第六章玄学的”组合证明“。而生成函数与组合证明，它们恰能够结合在一起。

//二项式定理？

比如Yanghui恒等式，可以这么证：$(1+ x)^n = (1 + x)^{n-1} + x (1 + x)^{n-1}$，关注左右式中$x^k$的系数即可。

又比如Vandermonde恒等式，关键的式子是$(1 + x)^{m + n} = (1 + x)^n (1 + x)^m$。

不难发现，使用生成函数的思路和组合证明的思路是完全一致的。但这个形式看起来就”正经“的多。

用生成函数解决组和问题

生成函数的模型

例1

$x_1 + x_2 + x_3 = 7$，其中$0 \leq x_1 \leq 2, 2 \leq x_2 \leq 3, 3 \leq x_4 \leq 4$，$x_1, x_2, x_3$为整数。求$(x_1, x_2, x_3)$有多少种可能。

例2

八本书，分给三个小孩，每人得到的书不少于两本不多于四本，求总方法数。

再谈可重复元素的组和

在讲这个例子前，先要提一提广义二项式定理。

广义二项式系数：$C_u^m = \dfrac{u \cdot (u-1) \cdot … \cdot (u - m + 1)} {1 \cdot 2 \cdot … \cdot m}$，其中m为非负整数，u为任意实数。

特别的，当u为负整数的时候，我们有$C_{-n}^m = (-1)^m C_{n + m - 1}^m$。

广义二项式定理：$(1 + x)^u = \sum\limits_{i = 0}^{\infty} C_u^i x^i$。（证明的话，幂级数展开就好）

例3

有n种硬币，每种有无穷多个，问取r个硬币有多少种方法。

第一种硬币可以取0个、1个、2个、……，这样考虑的话，生成函数便是$G(x) = (1 + x + …)^n$。

但无穷级数相乘很难算。我们为了能够算出结果，假定级数收敛，那么$(1 + x + …) = \dfrac{1} {1 - x}$。则$G(x) = \dfrac{1} {(1 - x)^n}$。

于是可以使用上面的广义二项式定理了，得$x^r$的系数是$C_{n + r - 1}^r$。

回过来再考虑生成函数的问题，它为何要是无穷级数？为了方便表示”可重复元素“，也是为了计算上的方便，因为这样就可以在微积分和组合数学之间建立联系了，从而使用微积分中的一些性质。而对于实际的问题，我们都可以在模$x^r$的意义下考虑原式子，这样让人困惑的无穷就消失啦。

为何能假定上面的式子收敛？我也不知道，好用就行了

例4

有三种硬币，币值分别为1、2、5，每种都有无穷个，求取r元有多少种方法？

用生成函数解决排列问题[需完善]

用生成函数解决递推问题[需完善]

考虑斐波那契数列的生成函数：$G(x) = \sum\limits_{i = 0}^{\infty} f_i x^i$，$G(x) = x + \sum\limits_{i = 2}^{\infty} f_i x^i = x + \sum\limits_{i = 2}^{\infty} (f_{i-1} + f_{i-2}) x^i = x + x\sum\limits_{i = 0}^{\infty} f_i x^i + x^2 \sum\limits_{i = 0}^{\infty} f_i x^i = x + xG(x) + x^2 G(x)$，则$G(x) = \dfrac{x} {1 - x - x^2}$，因式分解再裂项，就得到我们常见的结果了。

为什么生成函数这么奇妙？因为它巧妙地将递推关系用来消项。//然后我也讲不出什么道道了

这里的G(x)看起来是很抽象的，有没有办法让它表现得具体一点呢？您好，有的。我们来算一下$G(1/10) = \dfrac{10}{89} = 0.1123595506…$，不难发现小数点后第i项就是斐波那契数列第i项（仅限前几项，因为后面的要进位）。

如此，我们便可以用生成函数在小数和数列间建立联系啦，也可以用生成函数得到一些好玩的小数。

容斥原理[需补充]

内容

素数个数（关注计算复杂度）

满射的个数

错排问题

后面的部分引自网络，略有删改。（不知是否这位老哥原创的）

$\forall i, f(i) \not = i, i, f(i) \in \{ 1, 2, …, n \};\forall i \not = j, f(i) \not = f(j)$，求符合要求的函数个数D(n)。

核心递推公式：

$D(n) = (n-1) [D(n-2) + D(n-1)]$

初始值：$D(1) = 0, D(2) = 1$。

递推的推导错排公式

分析i = 1，它有n-1个取值。不失一般性，设$f(1) = 2$。再分析i = 2，若$f(2) = 1$，剩下的个数就是$D(n-2)$。

下面的一步就好玩了：如果$f(2) \not = 1$，那么剩下的个数是多少呢？注意！$f(2) \not = 1, f(3) \not = 3, …, f(n) \not = n$，这难道不是新的错排，个数是$D(n-1)$？于是，上面的递推式就得到啦！

下面咱们来推公式。

根据套路，设$D(n) = n! N(n)$，然后推一推，得//怎么想到要这么做的？

$nN(n) = (n-1) N(n-1) + N(n-2)$​，然后有

$N(n-1) - N(n-2) = (-1)^{n-1} / (n-1)!$，相加得

$N(n) = (-1)^2/2! + … + (-1)^{n-1} / (n-1)! + (-1)^n/n!$

故

$D(n) = n! [(-1)^2/2! + … + (-1)^{n-1}/(n-1)! + (-1)^n/n!]$

此即错排公式。

用容斥原理的推导

用容斥原理也可以推出错排公式:

正整数1, 2, 3, ……, n的全排列有 n! 种，其中第k位是k的排列有 (n-1)! 种;当k分别取1, 2, 3, ……, n时，共有n*(n-1)!种排列是至少放对了一个的，由于所求的是错排的种数，所以应当减去这些排列;但是此时把同时有两个数不错排的排列多排除了一次，应补上;在补上时，把同时有三个数不错排的排列多补上了一次，应排除……重复该一过程，得到错排的排列种数为

$D(n) = n! - n!/1! + n!/2! - n!/3! + … + (-1)^nn!/n! = ∑(k=2~n) (-1)^k n! / k!$，

即$D(n) = n! [1/0! - 1/1! + 1/2! - 1/3! + 1/4! + … + (-1)^n/n!]$.

简化公式

错排的公式里有n项，计算复杂度是O(n)，有没有简便的近似值呢，像Stirling公式一般？有的，而且不仅仅是近似值：$D(n) = \lfloor n!/e+0.5 \rfloor$。（但是这个公式有何意义呢？计算n!不还得O(n)？）

以下是证明：

对$1/e$幂级数展开一波，得$1/e = e^{-1} = 1/0! - 1/1! + 1/2! - 1/3! - ….. + (-1)^n/n! + R_n(-1)$//看不懂

其中$R_n(-1)$，$R_n(-1) = (-1)^{n+1} \cdot e^u / (n+1), u∈(-1, 0)$

所以，$D(n) = n! \cdot e^{-1} - (-1)^{n+1} \cdot e^u / (n+1), u∈(-1, 0)$

而$|n! R_n| = |(-1)^{n+1} \cdot \dfrac{e^u} {n+1}| = \dfrac{e^u} {n+1} ∈ (\dfrac{1} {[e(n+1)]}, \dfrac{1}{n+1})$，可知即使在n=1时，该余项(的绝对值)也小于1/2。

术语[需审核]

递推关系：recurrence relations

初始条件：initial conditions

线性常系数(非)齐次递推关系：linear (non)homogeneous recurrence relations with constant coefficients

关联的齐次递推关系：associated homogeneous recurrence relations（把F(n)去掉得到的递推关系）

特征方程/特征根：characteristic equation/roots

分治算法：divide-and-conquer algorithms

分治算法的递推关系：divide-and-conquer recurrence relation

最近点对问题：closest-pair problem

埃氏筛：sieve of Eratosthenes

错排：derangement

完稿于2019-05-01